poniedziałek, 9 kwietnia 2012

z fascynacji...


Ciąg Fibonacciego – ciąg liczb naturalnych określony rekurencyjnie w sposób następujący:
Pierwszy wyraz jest równy 0, drugi jest równy 1, każdy następny jest sumą dwóch poprzednich.
Formalnie:
F_n := \begin{cases} 0 & \mbox{dla } n = 0; \\ 1 & \mbox{dla } n = 1; \\ F_{n-1}+F_{n-2} & \mbox{dla } n > 1. \\ \end{cases}
Kolejne wyrazy tego ciągu nazywamy liczbami Fibonacciego. Kwestia, czy zaliczać zero do ciągu Fibonacciego, jest dyskusyjna. Część autorów rozpoczyna ciąg od F_1=1, F_2=1\;[1].
Wyrazy F_0,\dots, F_{19} ciągu Fibonacciego to:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181.
Ciąg został podany w 1202 roku przez Leonarda z Pizy zwanego Fibonaccim w swoim dziele Liber abaci jako rozwiązanie zadania o rozmnażaniu się królików. Nazwę "ciąg Fibonacciego" spopularyzował w XIX w. Édouard Lucas[2].
Autor: o

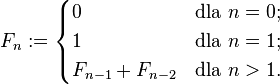
Brak komentarzy:

Prześlij komentarz

Subskrybuj: Komentarze do posta (Atom)